准确率、精确率和召回率
混淆矩阵 Confusion Matrix
什么是混淆矩阵
混淆矩阵是通过将预测标签与真实标签进行比较来总结分类模型性能的表格,它显示了模型预测的真正例(TP)、真负例(TN)、假正例(FP)和假负例(FN)的数量
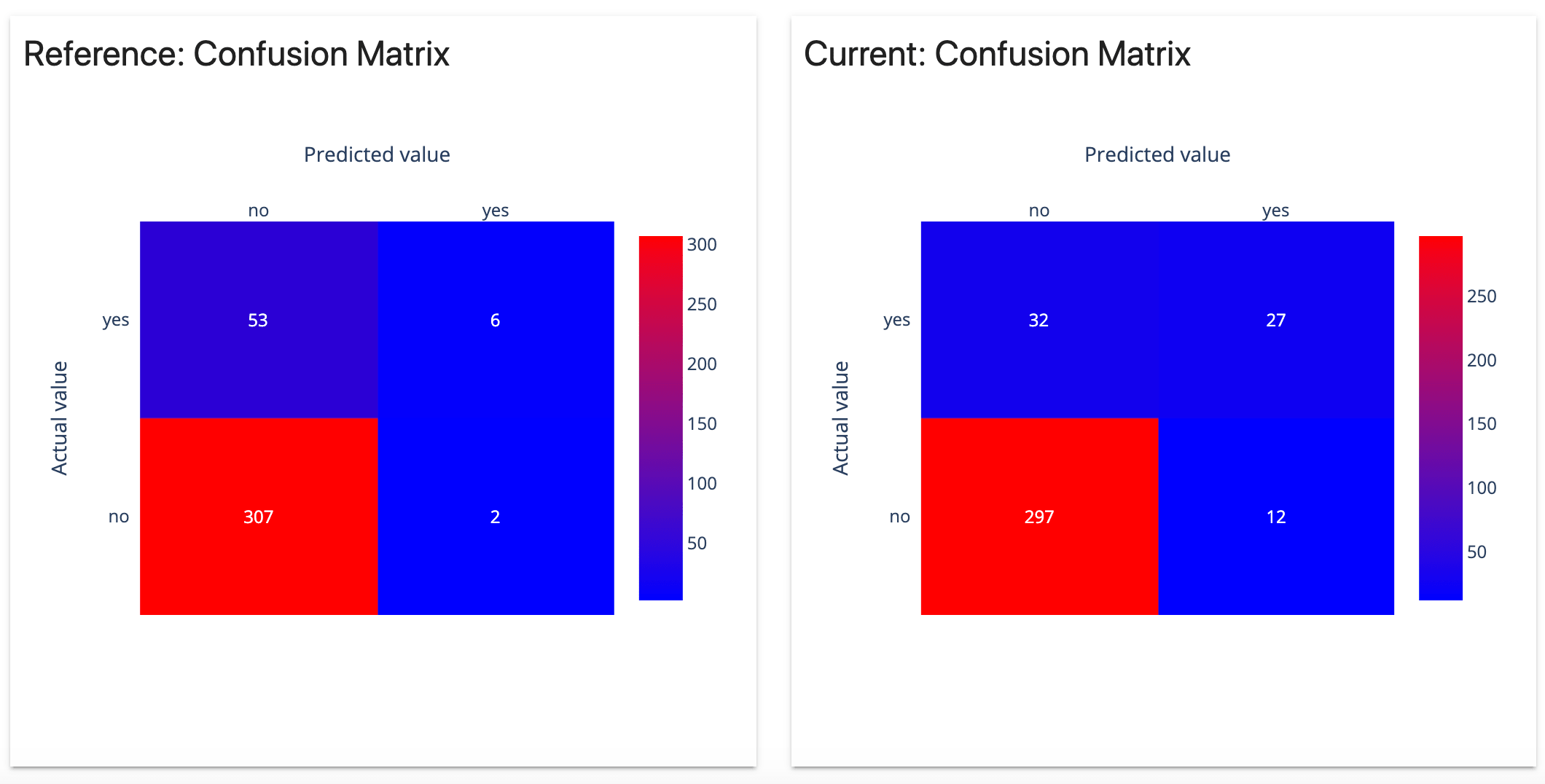
分类模型 Classification models
分类模型是一种机器学习模型,它为新的输入数据分配预定义的类别或标签
如果只有两个类别,则该分类是 binary 的;如果有多个类,则这是一个 multi-class 问题
混淆矩阵逻辑
创建一个混淆矩阵首先需要给出输入,模型给出预测的后给出实际标签
这样就可以判断出模型预测的正确性
一旦知道了实际的标签,就可以计算模型正确或错误的次数

错误类型
可以计算出不同错误类型的数量
- 误报 false alarm,将普通交易标记为欺诈
- 错过 miss,将欺诈交易标记为普通交易
第一种错误被称为 FP,第二种错误被称为 FN
positive 和 negative
positive 和 negative 针对的是目标和非目标分类
在上面例子中,交易欺骗是我们的目标分类,所以我们将交易欺骗认为是 positive
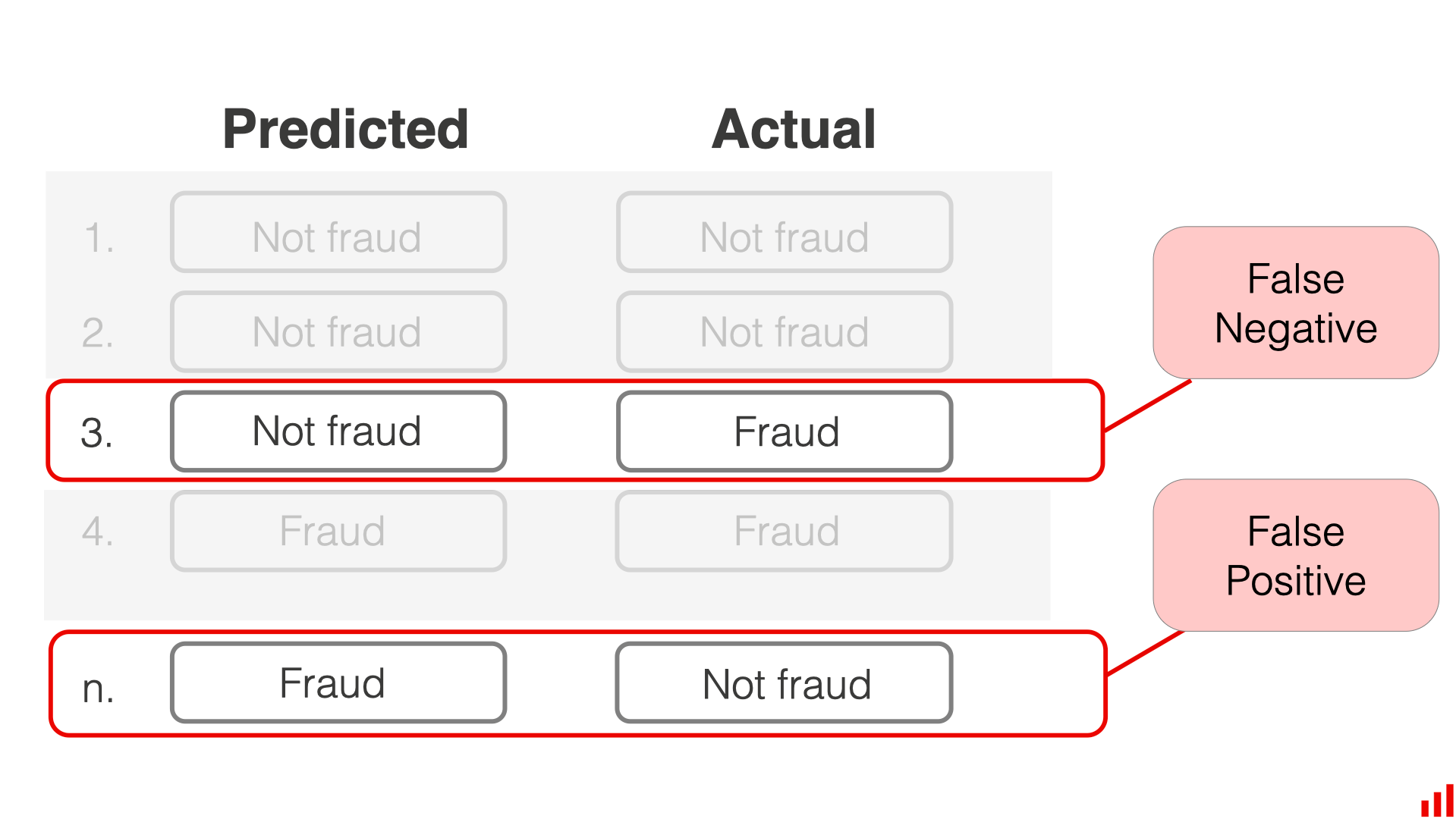
之所以要区分两种不同的错误类型,是因为在一些业务中两种错误的后果危害性不同

正确类型
同时也有两种不同的正确类型
- 检测出实际的欺骗行为
- 正确标记正常行为
第一种类型称为 TP,第二种行为称为 TN

检测出不同的正确类型是必要的,因为业务可能更感兴趣的是模型识别欺骗交易的能力,而不是模型总体正确的频率

总之对于一个预测模型,其得出的结果是如下四种之一
- 真正例(True Positive, TP):被模型预测为正的正样本
- 假正例(False Positive, FP):被模型预测为正的负样本
- 假负例(False Negative, FN):被模型预测为负的正样本
- 真负例(True Negative, TN):被模型预测为负的负样本
于是可以根据上述结果绘制出混淆矩阵,横坐标代表预期分类,纵坐标代表实际分类

阅读混淆矩阵
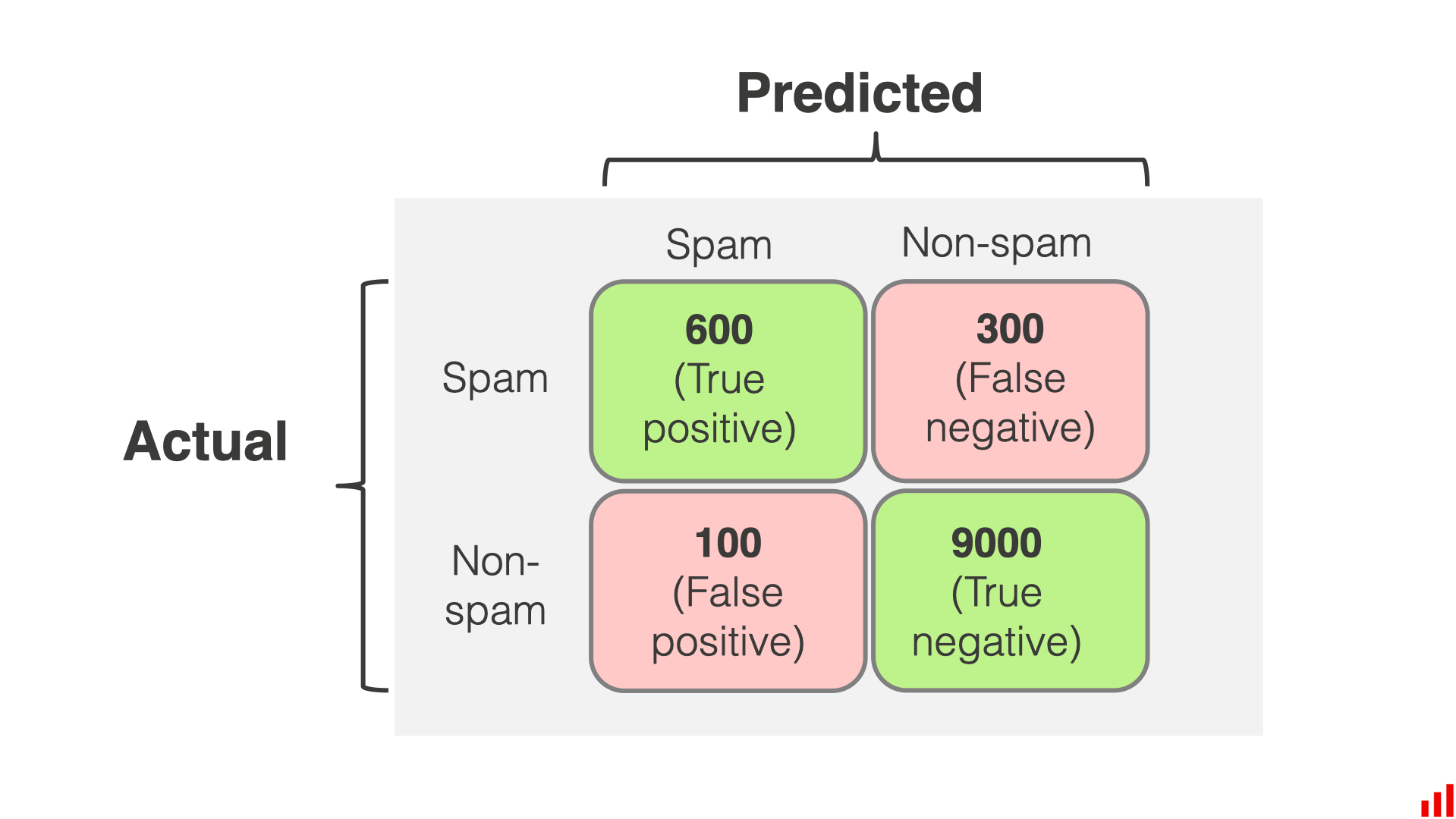
用一个场景举例,垃圾邮件分类;这是一个二元分类模型,可以得出 “是垃圾邮件” 和 “非垃圾邮件” 的分类

TP
- 左上角绿色区域
TN
- 右下角绿色区域
FP
- 右上角红色区域
FN
- 左下角红色区域
分类的质量指标
混淆矩阵可以给出预测正确、错误的绝对值(absolute number),但有时会希望衡量模型效果的相对值(relative)
以下是一些常用的指标来衡量分类模型的性能
- 准确率 Accuracy:模型总体上正确的比率
- 精确率 Precision:预测正例中正确的比率
- 召回率 Recall 或 true positive rate (TPR):预期正例中正确的比率
多分类的混淆矩阵
多类分类也遵循同样的逻辑,在这种情况下矩阵将会有两个以上的行和列
假设将用户评论分为三类:“负面”、“正面” 和 “中性”,下面是该问题的混淆矩阵示例
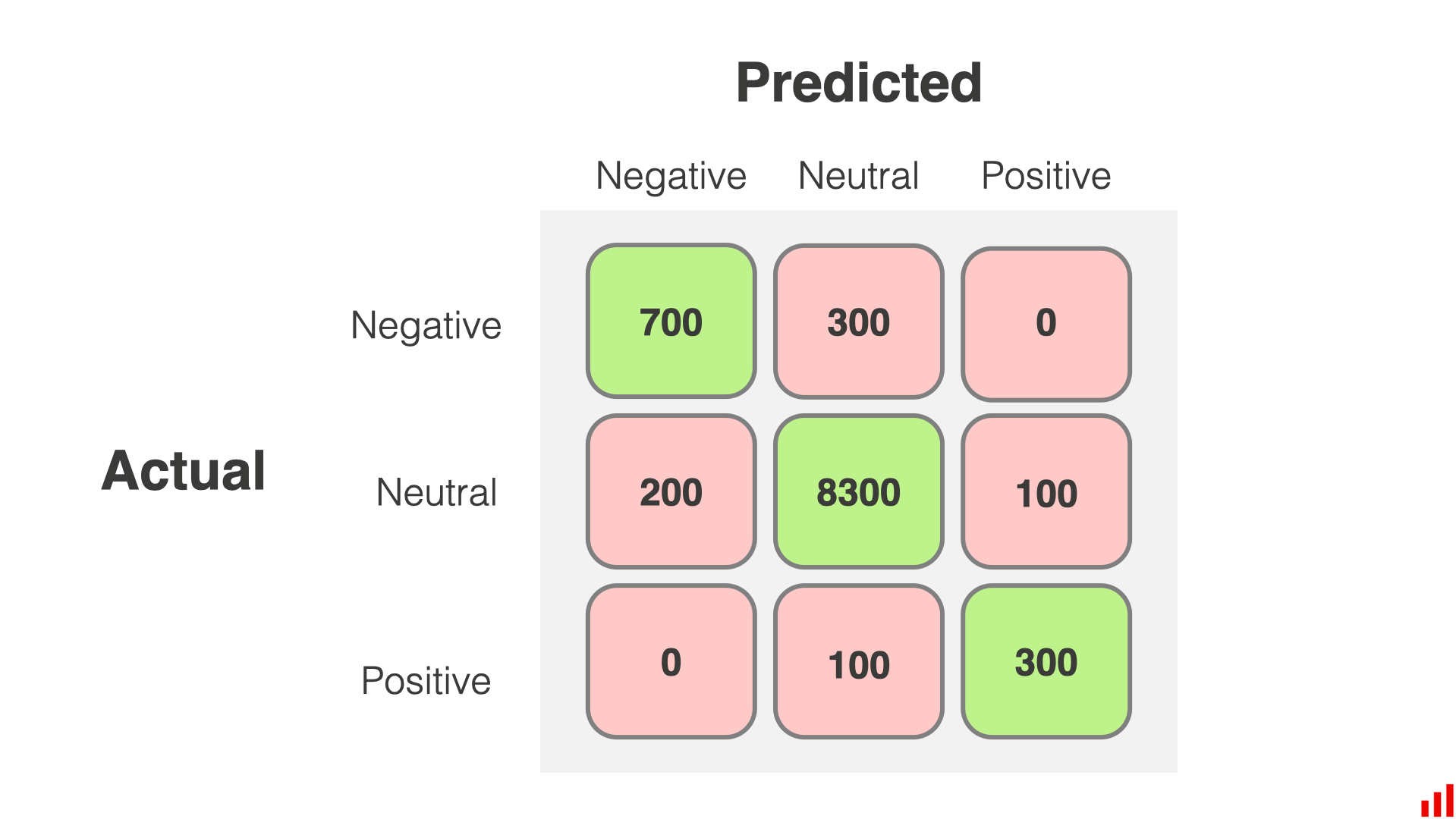
如何阅读
- 对角线代表正确分类的数据
- 第一行,模型正确地标记了 700 条(共 1000 条)负面评论,将 300 条错误地归类为中心评论
- 第二行,该模型正确地标记了 8300 条(共 8600 条)中性评论,但错误地将 200 条归类为负面评论,100 条归类为正面评论
- 第三行,该模型正确预测了 300 条(共 400 条)正面评论,但将 100 条错误地归类为中性评论
指标
准确率 Accuracy
模型正确的比率有多高
How often the model is right

混淆矩阵图示
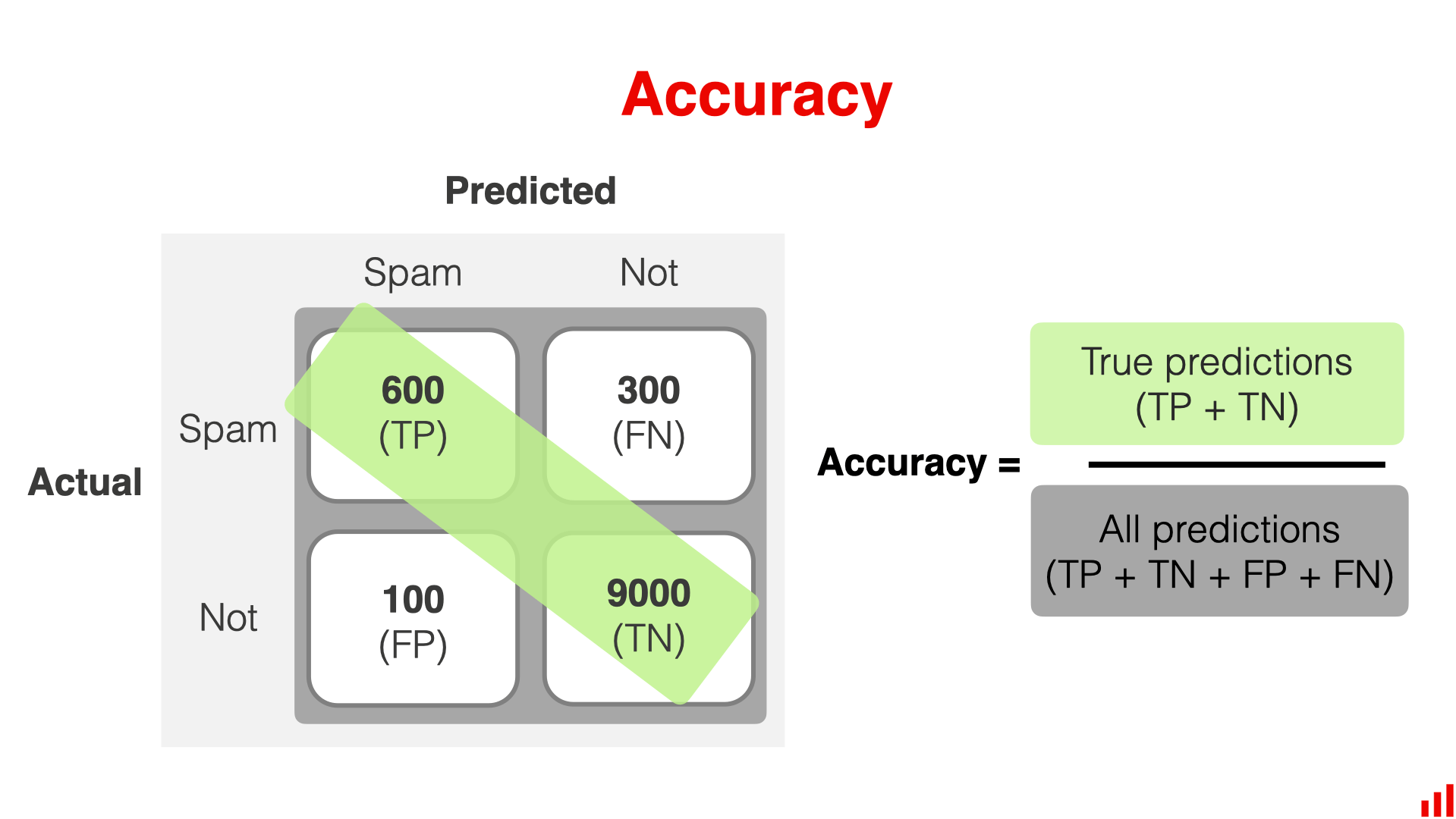
示例
有以下数据
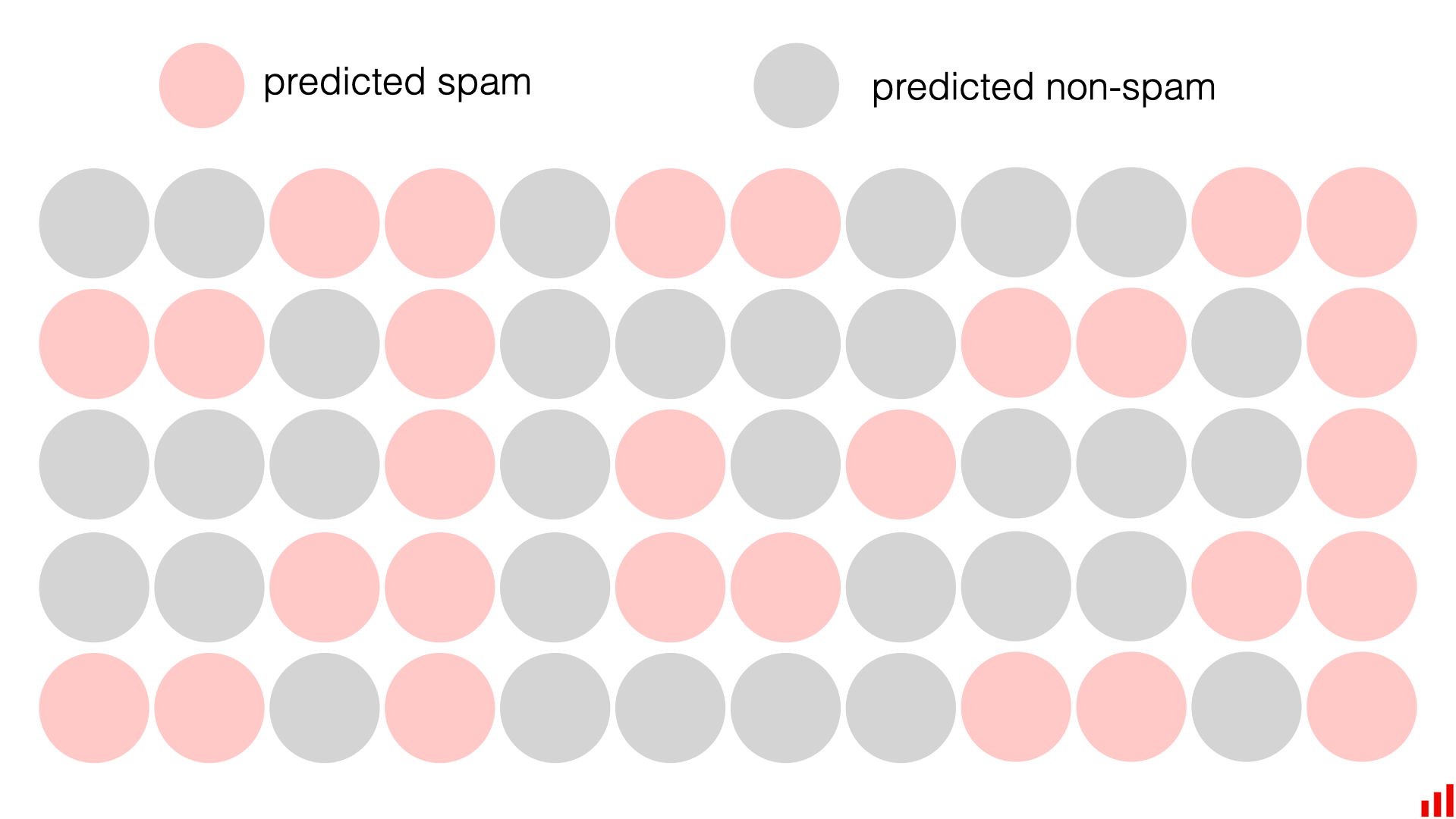
获取到预测结果后可以标注出正确性

可以简单地计算模型正确的次数,然后除以预测的总数
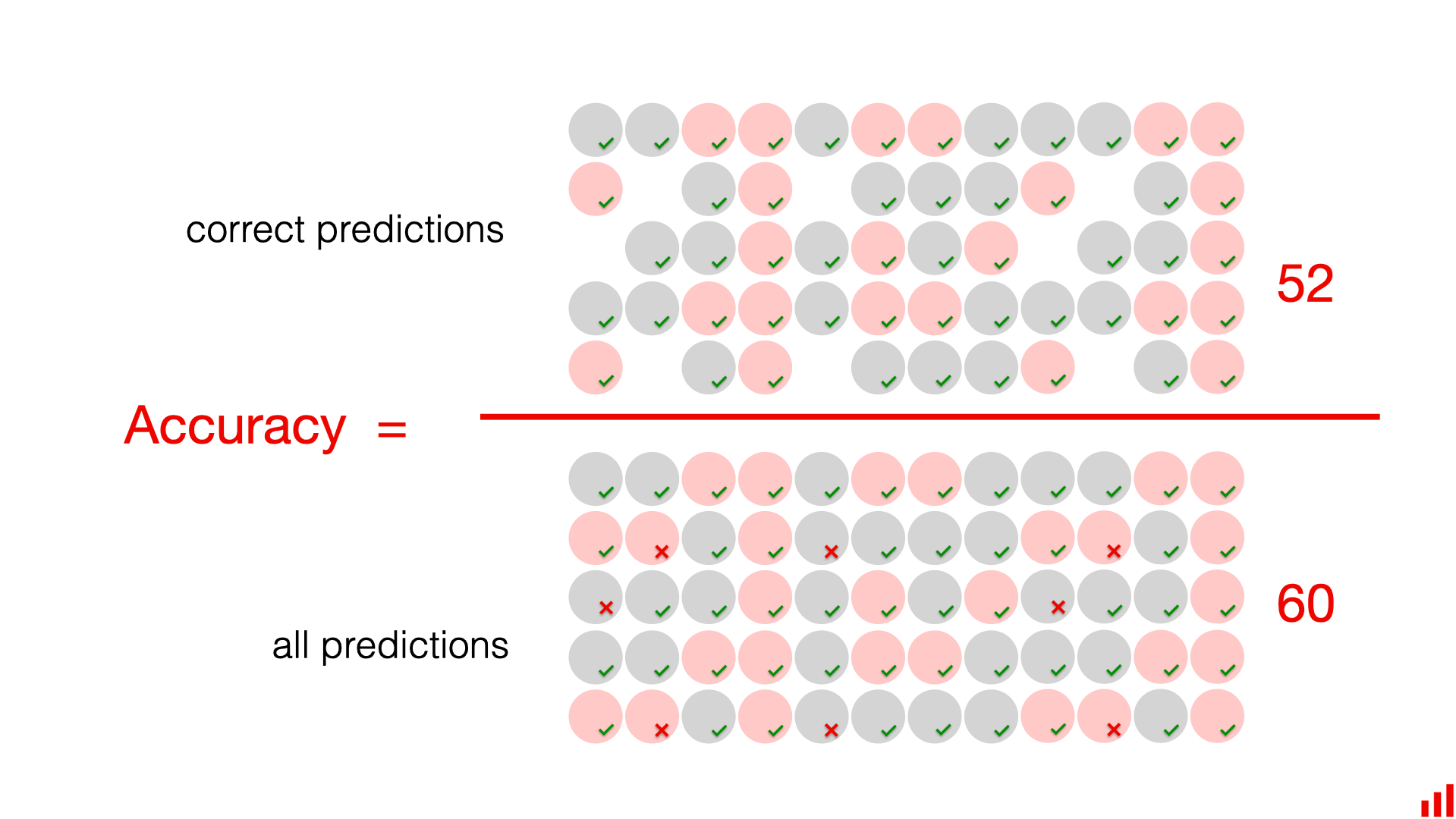
直观来看,准确性是判断模型质量的直接方法,它表示了模型整体的正确性,易于沟通
事实上这种措施并不总是有效,因为 accuracy paradox 准确性悖论存在
优缺点
- 优点
- 当关注平衡类别(balanced classes)并且关心整体模型的 “正确性” 而不是预测特定类别的能力时,是一个有用的指标
- 易于解释
- 缺点
- 如果类别不均衡,准确率的用处就会降低,因为它对模型预测所有类别的能力给予了同等的权重;在这种情况下,传达准确性可能会产生误导,并掩盖目标类别上的低性能
精确率 Precision
多少正例的预测是正确的
How often the positive predictions are correct
预测为正样本的结果中,真正为正样本的比例

混淆矩阵图示
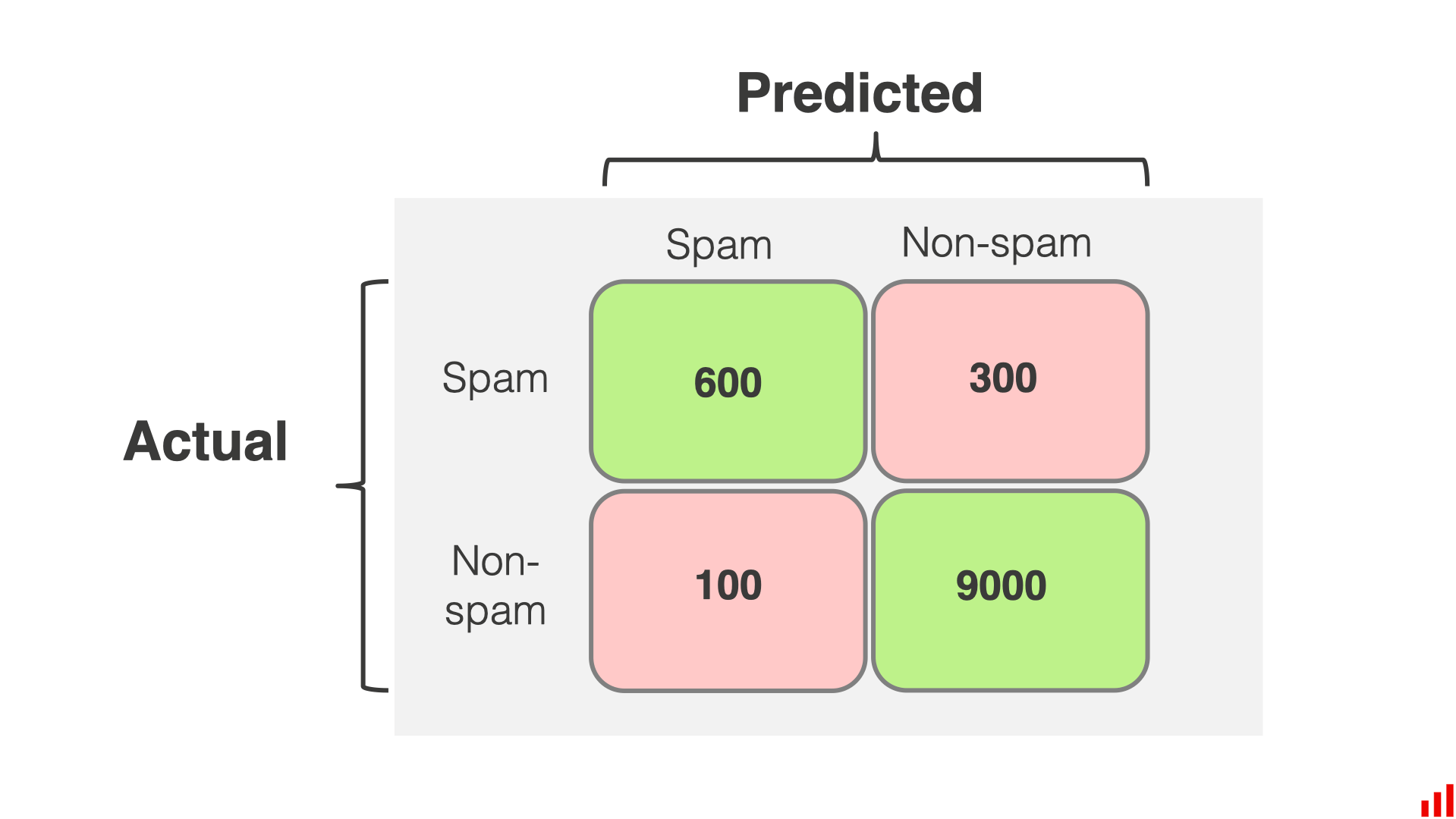
示例
邮件示例中假设有一个不平衡问题,只有 5% 的邮件是垃圾邮件

假设预测所有电子邮件都是非垃圾邮件

此时准确率为 95%(60 个 cases,模型有 57 个是准确的),但是精确率却为 0%
为了计算精确率,我们必须用 正确预测的垃圾邮件数量 除以 垃圾邮件总数;然而正确识别的垃圾邮件数量为 0,数据集中有 3 封垃圾邮件,但模型全部错过了,所有正确的预测都是关于非垃圾邮件的,精确率指标纠正了准确率的主要缺点

假设我们又训练了一个模型,得到的结果如上
此时准确率依然为 95%
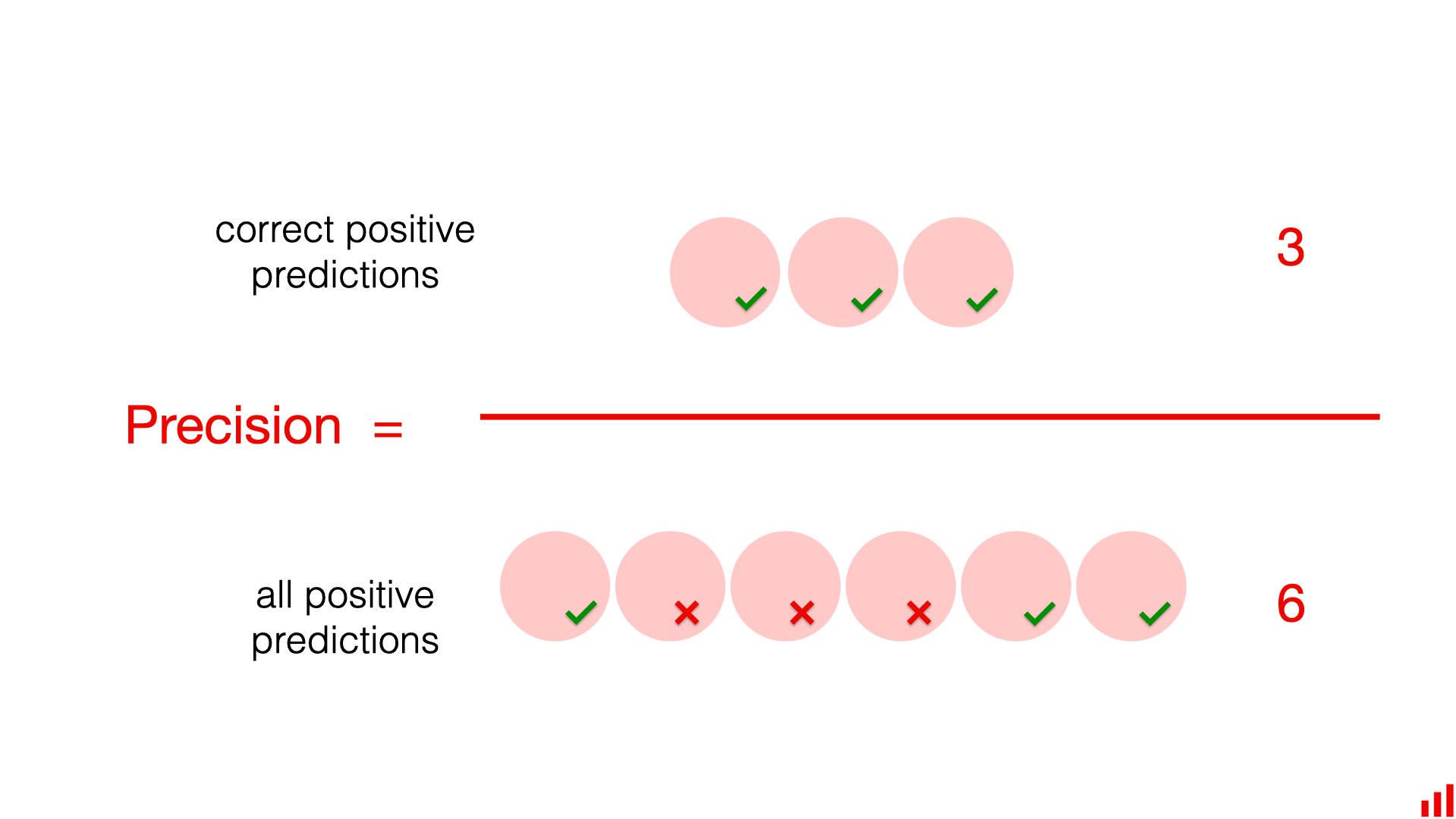
而精确率为 50%,该模型将 6 封电子邮件标记为垃圾邮件,并且有一半的时间是正确的。在标记为垃圾邮件的 6 封电子邮件中,实际上有 3 封是垃圾邮件(真正的阳性),另外 3 封是错误标记(假阳性)
优缺点
什么时候精确率是一个适合关注的指标?
以下是精确率指标的优点:
- 对于类别不平衡的问题效果很好,因为它显示了模型在识别目标类别时的正确性
- 当误报成本很高时,精确率很有用。在这种情况下,即使遗漏了一些(或很多)实例,你通常也希望对识别目标类别有信心
假设这样一个产品需求,作为垃圾邮件检测功能的产品经理,认为误报错误的成本很高;可以将错误成本解释为由于错误预测而导致的负面用户体验;希望确保用户永远不会因为重要邮件被错误标记为垃圾邮件而错过它,这是一种错误最小化的需求,精确率是一个很好的评估和优化指标
较高的精确率得分表明模型做出的误报预测更少
在这种情况下,一些垃圾邮件可能会未被检测到并进入用户的收件箱,此时会认为这种类型的错误(漏报)的成本更可容忍,用户仍然可以手动将这些邮件标记为垃圾邮件,但是每当自动将邮件放入垃圾邮件文件夹并对用户隐藏时,它们最好确实是垃圾邮件
当然精确率也有缺点:
- 精确率不考虑假阴性,即它没有考虑我们错过目标事件的情况
这就是为什么需要另一个指标来平衡精确率:召回率
召回率 Recall
模型是否能够识别出所有的正例
所有正样本中,被正确预测为正例的比例,考虑了假阴性

可以在 0 到 1 的范围内或用百分比来衡量召回率;召回率越高越好,当模型能够在数据集中找到目标类的所有实例时,可以实现完美召回率为 1.0
召回率也可以称为敏感度或真正例率。“敏感度” 一词在医学和生物学研究中比在机器学习中更常用;例如,可以参考医学诊断测试的敏感度来解释其正确揭示大多数真正例的能力,概念是相同的
混淆矩阵图示
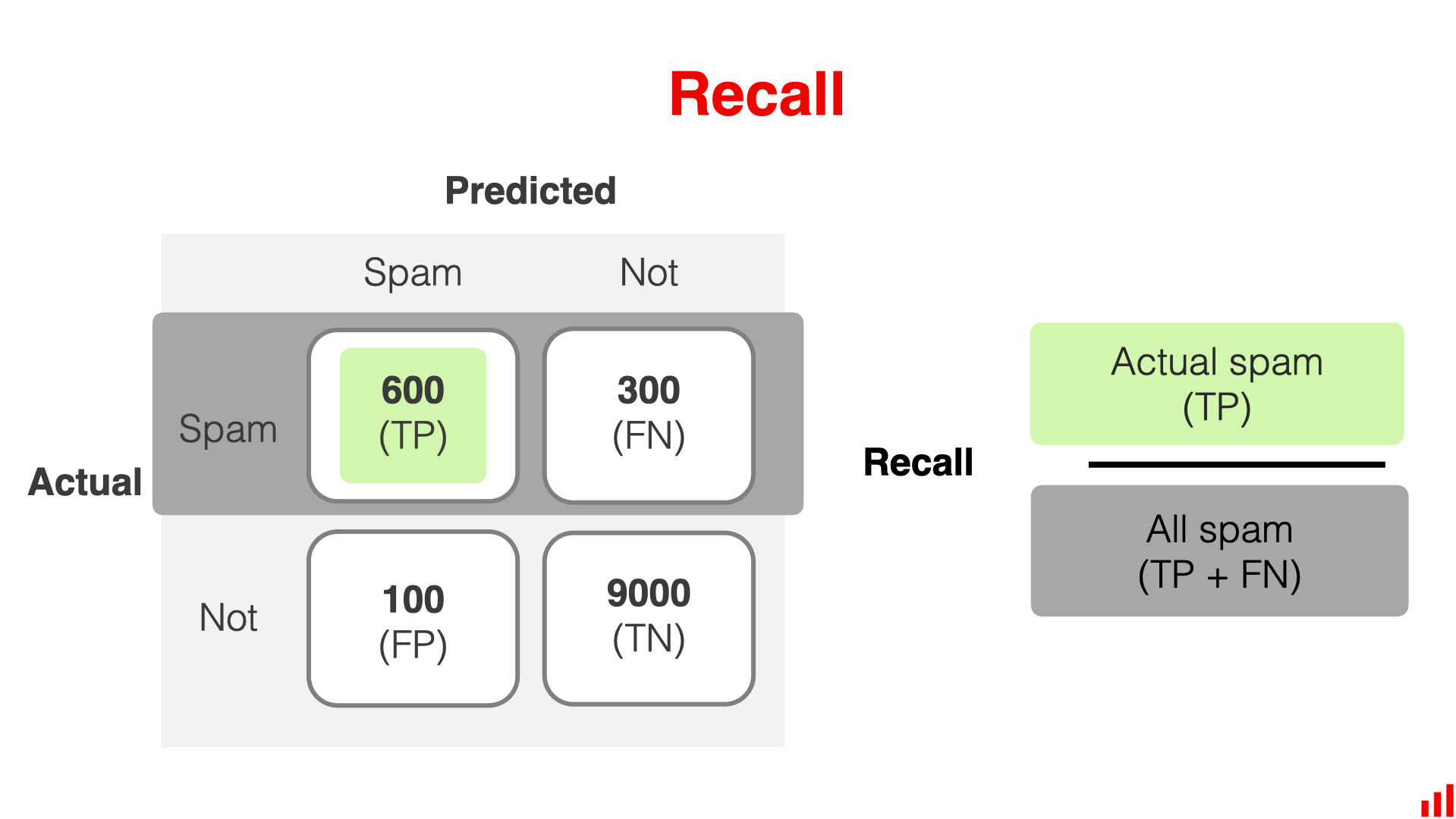
示例
依然用识别垃圾邮件举例

如之前的模拟情况为例,此时我们知道准确率为 95%,精确率为 50%
要计算召回率,我们必须用已发现的垃圾邮件数量除以数据集中垃圾邮件的总数
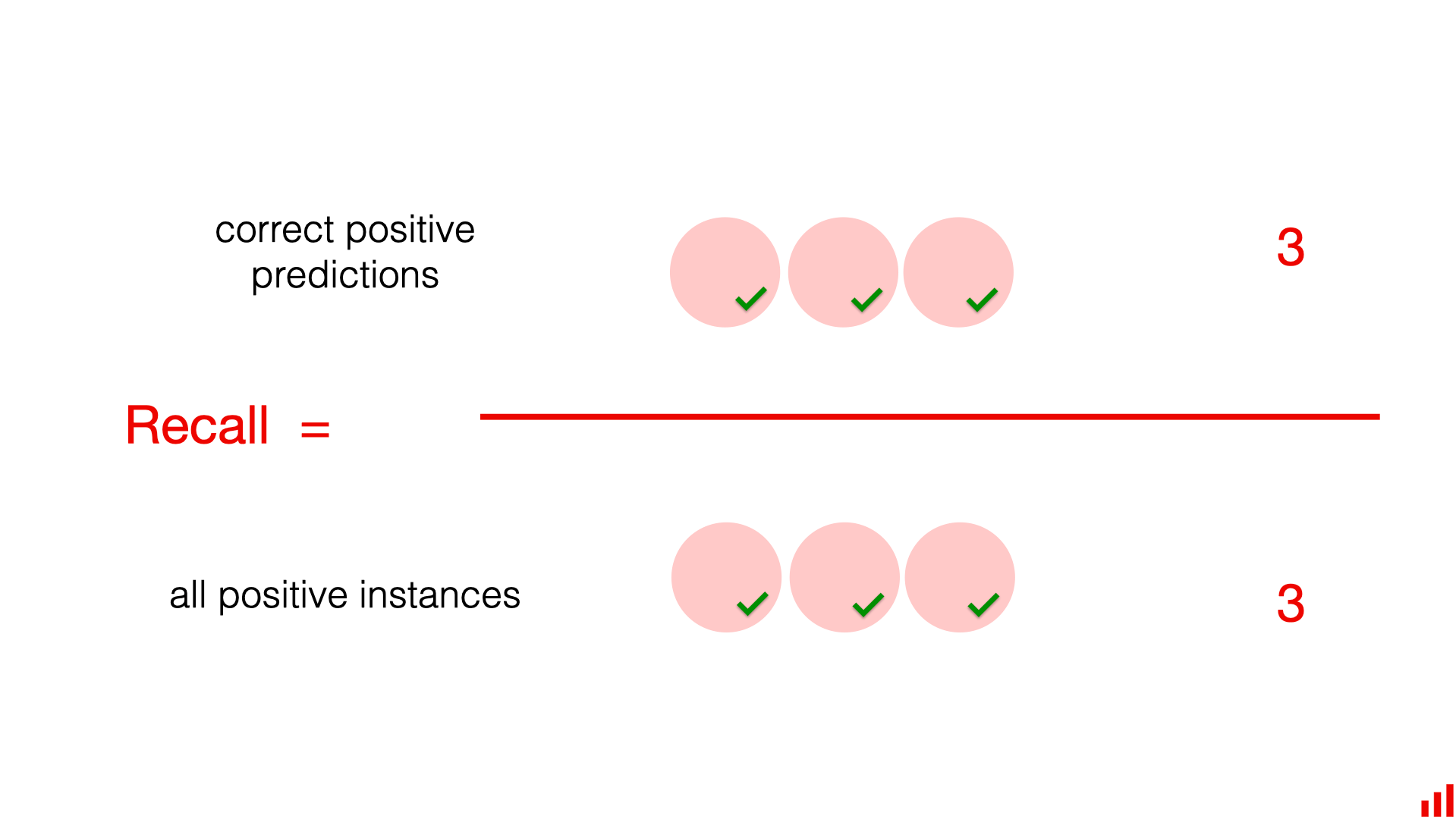
召回率为 100%。数据集中有 3 封垃圾邮件,模型找到了所有这些邮件
这样,召回率展现了模型质量的又一个维度;总之这个虚构的模型具有 95% 的准确率、50% 的精确率和 100% 的召回率
优缺点
- 优点
- 它对于具有类别不平衡的问题很有效,因为它专注于模型找到目标类对象的能力
- 当假阴性成本很高时,召回率很有用;在这种情况下,通常希望找到目标类的所有对象,即使这会导致一些误报(当实际上为阴性时预测为阳性)
- 缺点
- 它没有考虑误报(false positives)的成本 误报的成本可能仍然很高。在极端情况下,如果需要审查的决策过多且精度较低,它们可能会使模型变得毫无用处
召回率的极端情况与准确率悖论相反:如果想实现 “完全召回”,可以将每个对象都标记为可疑
例如可以将每封电子邮件都标记为垃圾邮件,这样就实现了 100% 的召回率,但绝大多数预测将是误报,从而使模型变得毫无用处
没有单一的指标是完美的,因此同时考虑多个指标并在精度和召回率之间确定适当的平衡是有意义的
实践
由于没有一个指标能反映出衡量模型质量的 “绝对最佳” 方法,因此通常需要综合考虑这些指标,或者有意识地选择更适合特定场景的指标
在确定哪种指标更合适时,这里有一些需要牢记的注意事项
注意类别平衡
在解释精确率、召回率和准确率时,评估类别比例并记住每个指标在处理不平衡类别时的表现是有意义的。一些指标(如准确率)可能看起来具有误导性地好,并掩盖重要少数类别的性能

注意误判的成本
精度是在分配正类时更关心 “正确分类” 而非 “全部检测出” 的情况下的一个合适指标
召回率指标则相反
注意决策阈值
在精度和召回率之间找到正确平衡的另一种方法是手动为概率分类设置不同的决策阈值
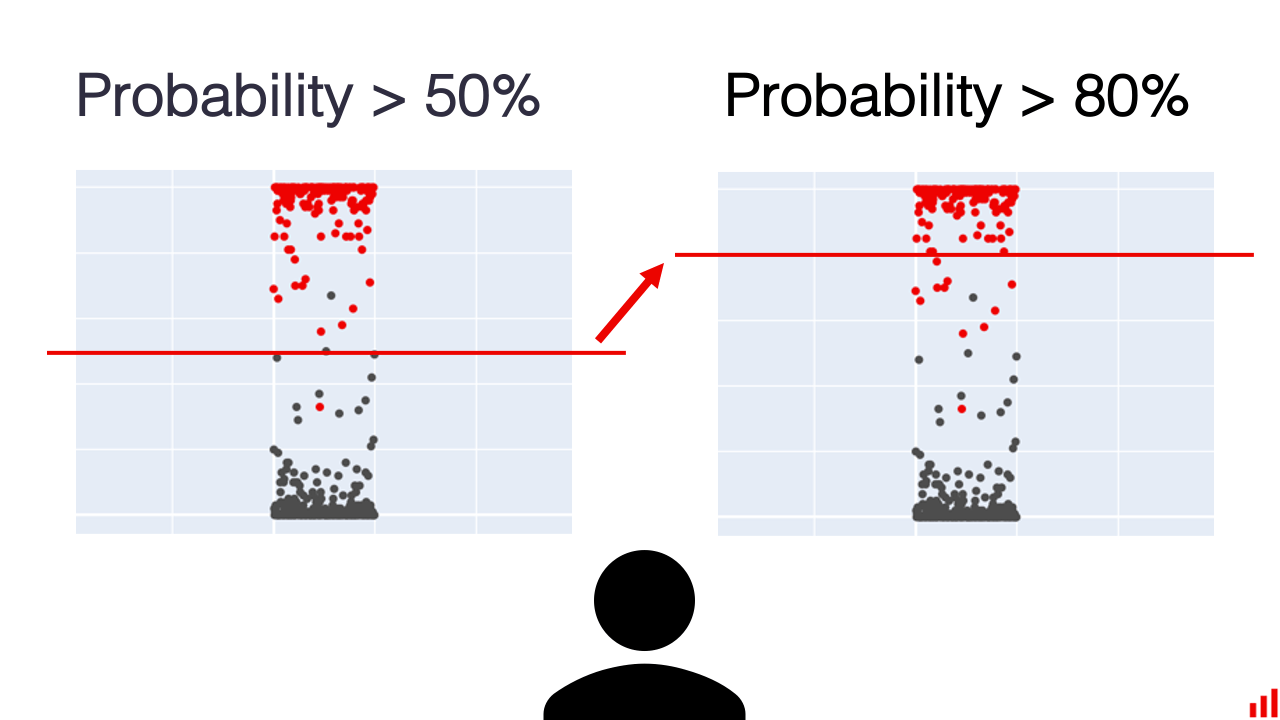
决策阈值是一个值,当输入值高于该值时,输入被分类为属于特定类别;当输入值低于该值时,输入被分类为属于不同类别
例如,当预测概率为 0.5 时,可以将预测分配给特定类别,或者将其调整为 0.8
如果目标是最小化误报(最大化精确率),那么较高的决策阈值可能更合适;另一方面,如果目标是最小化漏报(最大化召回率),那么较低的决策阈值可能更合适
参考
Evidently AI - Classification metrics guide
Accuracy vs. precision vs. recall in machine learning: what's the difference?